欺负抛物线好计算的一个小练习（抛物线原理的计算）

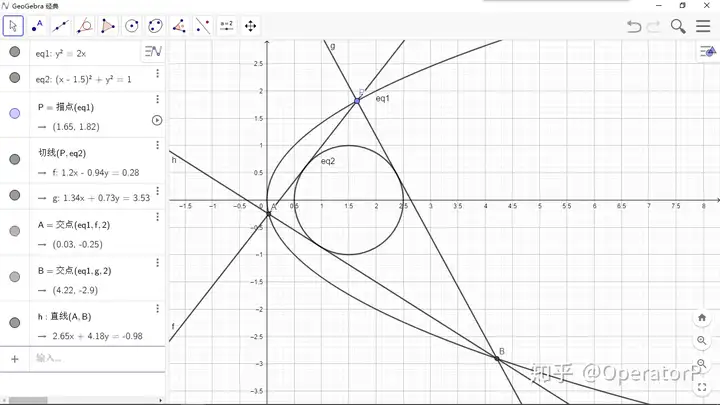
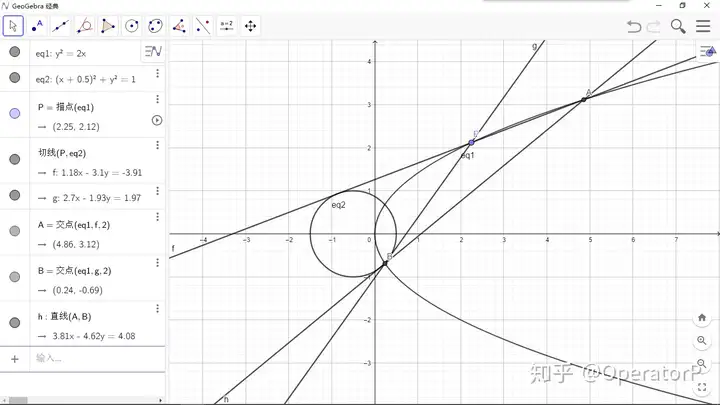
探究：已知抛物线，一个圆。抛物线上有一个动点，过做圆的两切线，分别交抛物线于，。求直线与定圆相切的条件。探究：已知抛物线y2=2px，一个圆(x−x0)2+y2=r2。抛物线上有一个动点P，过P做圆的两切线PA，PB分别交抛物线于A，B。求直线AB与定圆相切的条件。探究：已知抛物线y^2=2px，一个圆(x-x_0)^2+y^2=r^2。\\ 抛物线上有一个动点P，过P做圆的两切线PA，PB分别交抛物线于A，B。\\ 求直线AB与定圆相切的条件。

计算：不妨设。若方程为，方程为，我们有：将此方程与抛物线方程联立消去并整理得到联系经过一次，也经过一次，纵坐标可分解此式得于是我们知道直线与抛物线联立消去后的方程为将抛物线方程用来反向消去二次项即得到方程为不妨设所切圆的圆心，半径，则由点到直线距离公式得变形得由题意知此等式成立与无关，故三个系数均为零。将第三个方程两边平方并用前两个式子带入消去和得展开得计算：不妨设P(t22p,t)。若PA方程为l1=0，PB方程为l2=0，我们有：l1l2=0⇔r2[(x−t22p)2+(y−t)2]=[tx+(x0−t22p)y−x0t]2将此方程与抛物线方程联立消去x并整理得到(t2−r2)y4+2t(2px0−t2)y3+[(2px0−t2)2−4px0t2−2r2(2p2−t2)]y2+4pt[2r2p−x0(2px0−t2)]y+t2(4p2x02−4p2r2−r2t2)=0联系l1经过一次P，l2也经过一次P，P纵坐标t可分解此式得(y−t)2[(t2−r2)y2+2t(2px0−r2)y+4p2(x02−r2)−r2t2]=0于是我们知道直线AB与抛物线联立消去x后的方程为(t2−r2)y2+2t(2px0−r2)y+4p2(x02−r2)−r2t2=0将抛物线方程用来反向消去二次项y即得到AB方程为2p(t2−r2)x+2t(2px0−r2)y+4p2(x02−r2)−r2t2=0不妨设AB所切圆的圆心(x′,0)，半径d，则由点到直线距离公式得|2p(t2−r2)x′+4p2(x02−r2)−r2t2|4p2(t2−r2)2+4t2(2px0−r2)2=d变形得[4d2p2−(2px′−r2)2]t4+4[d2(2px0−r2)2−2d2p2r2−p(2px′−r2)(2px02−2pr2−r2x′)]t2+4p2[d2r4−(2px02−2pr2−r2x′)2]=0由题意知此等式成立与t无关，故三个系数均为零。4d2p2=(2px′−r2)2d2r4=(2px02−2pr2−r2x′)2d2[(2px0−r2)2−2p2r2]=p(2px′−r2)(2px02−2pr2−r2x′)将第三个方程两边平方并用前两个式子带入消去d和x′得[(2px0−r2)2−2p2r2]2=4p4r4展开得(2px0−r2)4=4p2r2(2px0−r2)2计算：不妨设P(\frac{t^2}{2p},t)。\\ 若PA方程为l_1=0，PB方程为l_2=0，我们有：\\ l_1l_2=0\Leftrightarrow r^2[(x-\frac{t^2}{2p})^2+(y-t)^2]=[tx+(x_0-\frac{t^2}{2p})y-x_0t]^2\\ 将此方程与抛物线方程联立消去x并整理得到\\ (t^2-r^2)y^4+2t(2px_0-t^2)y^3+[(2px_0-t^2)^2-4px_0t^2-2r^2(2p^2-t^2)]y^2\\+4pt[2r^2p-x_0(2px_0-t^2)]y+t^2(4p^2x_0^2-4p^2r^2-r^2t^2)=0\\ 联系l_1经过一次P，l_2也经过一次P，P纵坐标t可分解此式得\\ (y-t)^2[(t^2-r^2)y^2+2t(2px_0-r^2)y+4p^2(x_0^2-r^2)-r^2t^2]=0\\ 于是我们知道直线AB与抛物线联立消去x后的方程为\\ (t^2-r^2)y^2+2t(2px_0-r^2)y+4p^2(x_0^2-r^2)-r^2t^2=0\\ 将抛物线方程用来反向消去二次项y即得到AB方程为\\ 2p(t^2-r^2)x+2t(2px_0-r^2)y+4p^2(x_0^2-r^2)-r^2t^2=0\\ 不妨设AB所切圆的圆心(x,0)，半径d，则由点到直线距离公式得\\ \frac{|2p(t^2-r^2)x+4p^2(x_0^2-r^2)-r^2t^2|}{\sqrt{4p^2(t^2-r^2)^2+4t^2(2px_0-r^2)^2}}=d\\ 变形得\\ [4d^2p^2-(2px-r^2)^2]t^4+\\4[d^2(2px_0-r^2)^2-2d^2p^2r^2-p(2px-r^2)(2px_0^2-2pr^2-r^2x)]t^2\\ +4p^2[d^2r^4-(2px_0^2-2pr^2-r^2x)^2]=0\\ 由题意知此等式成立与t无关，故三个系数均为零。\\ 4d^2p^2=(2px-r^2)^2\\ d^2r^4=(2px_0^2-2pr^2-r^2x)^2\\ d^2[(2px_0-r^2)^2-2p^2r^2]=p(2px-r^2)(2px_0^2-2pr^2-r^2x)\\ 将第三个方程两边平方并用前两个式子带入消去d和x得\\ [(2px_0-r^2)^2-2p^2r^2]^2=4p^4r^4\\ 展开得\\ (2px_0-r^2)^4=4p^2r^2(2px_0-r^2)^2

验算：我们对这个式子可能的两组解分别讨论。情况一：。此时带回知方程为显然这是一条与轴垂直的动直线，不合题意。情况二：。此时带回知恰好有，即三角形的内切圆恒定。验算：我们对这个式子可能的两组解分别讨论。情况一：2px0=r2。此时带回知AB方程为x=x0t2+4p2x0−2px02t2−r2显然这是一条与x轴垂直的动直线，不合题意。情况二：(2px0−r2)2=4p2r2。此时带回知恰好有x′=x0，d=r即三角形PAB的内切圆恒定。验算：我们对这个式子可能的两组解分别讨论。\\ 情况一：2px_0=r^2。此时带回知AB方程为\\ x=\frac{x_0t^2+4p^2x_0-2px_0^2}{t^2-r^2}\\显然这是一条与x轴垂直的动直线，不合题意。\\ 情况二：(2px_0-r^2)^2=4p^2r^2。此时带回知恰好有\\ x=x_0，d=r\\ 即三角形PAB的内切圆恒定。

情况二固定一个参数会对应出两个圆，一个在内一个在外。

备注：这个东西可以视作两个定理的退化。

1、Poncelet闭合定理（平面上给定两条圆锥曲线，若存在一封闭多边形外切其中一条圆锥曲线且内接另一条圆锥曲线，则此封闭多边形内接的圆锥曲线上每一个点都是满足这样（切、接）性质的封闭多边形的顶点，且所有满足此性质的封闭多边形的边数相同。）的三角形特殊情况（外抛物线内圆）。

2、二次曲线上的点射影变换X->X，则直线XX包络另一个二次曲线，反之亦然（二次曲线的定向切线族在另一个二次曲线上 诱导出一个射影变换）。用这个圆诱导出变换A->P和P->B，则显然变换A->B也是一个射影变换，则AB与另一个定二次曲线相切。此处只是取了这个二次曲线为圆的特殊情况。

2021.7.14更新

哈哈，打中甲卷解析几何题了